ERC EXACTC
About EXACTC
The fundamental laws of nature, to the best of our knowledge, are described by the Standard Model of particle physics, which is based on Quantum Field Theory (QFT). QFTs are quantum mechanical systems with an infinite number of degrees of freedom. The quantum systems are in general incredibly complicated to study. Even for one degree of freedom we face a second order differential equation, which can be solved analytically in only a few cases. For a system of a few particles one needs supercomputers to solve the Schrödinger equations approximately. Therefore, dealing with infinitely many degrees of freedom in QFT is a problem of extreme complexity. The aim of this project is to find the complete solution of a fully interacting 4D QFT for the first time using integrability.
For more than 70 years a lot of effort was spent trying to efficiently get physical predictions from QFTs. Nevertheless, we still have a rather fragmented and often only qualitative knowledge of the physical picture. This is because most analytical calculation methods in QFTs are largely based on the weak coupling perturbation expansion or through Monte-Carlo simulations, which require costly computer simulations with rather limited precision.
Recently a new set of ideas based on integrability and holography were introduced.
Integrability was first introduced for mechanical systems, where the existence of extra integrals of motion frequently allowed one to get solutions in a closed form. When our QFT is integrable one can hope to be able to access physical results completely non-perturbatively at finite values of the system’s parameters. This is extremely complex and requires case-by-case investigation, but is worth it due to the potential to find incredibly powerful results. Until recently, all known integrable techniques applicable to QFTs were limited to 2D. Using holography one can then map a more realistic 4D QFT (3 space + 1 time) to a 2D world sheet and thus apply the integrability methods to access new physical phenomena.
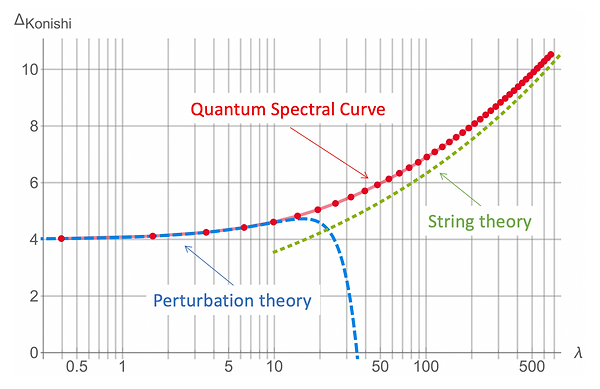
The PI was responsible for several breakthroughs in the field of integrability and holography. In one of them, the PI managed to solve a major problem: finding the spectrum – or equivalently the two-point correlation functions – of these theories. With his collaborators, he pioneered a ground-breaking discovery: they found exact equations for the spectrum of simple but highly non-trivial excited string states (published and highlighted by editors in Phys. Rev. Lett.). This powerful set of equations became known as the Quantum Spectral Curve (QSC).
The project is dedicated to pushing those exciting developments to the next level – by combining the QSC with the powerful method of Separation of Variables, which we believe will allow us to gain access to all physically relevant quantities in this class of QFTs. In turn, this would constitute the solution of a 4D QFT for the first time – which is the aim of this project.
We have made a lot of progress on the project in the last two years. The work can be divided into 3 directions: the formal mathematical approach; approaching the problem from the QFT side; and exploring further applications of our methods – i.e. stretching beyond what we could initially foresee.
Separation of Variables
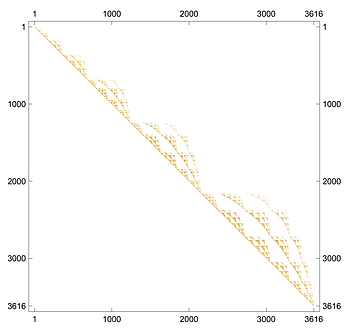
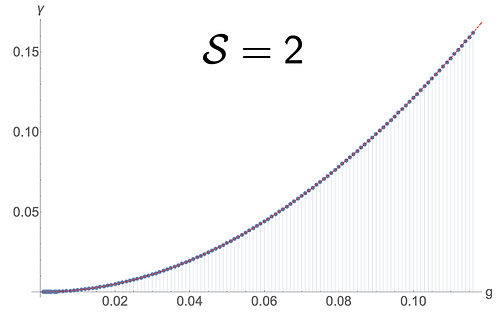
Formal mathematical approach: This approach deals with more general integrable models, such as spin-chains. This is an incredibly rich class of integrable models which also includes some 4D QFTs such as Fishnet and N=4 Super Yang-Mills as a particular case. My team and I have been developing novel methods of separation of variables. This method allows us to greatly simplify the wave function of this many-body quantum system by essentially reducing the problem to a set of much simpler one-particle problems. It is known that the wave function is the fundamental object in quantum mechanics which contains full information about the state of a quantum system and allows one to compute all physically relevant characteristics. However, in general it is not guaranteed that the expression for the physically important quantities is simple in terms of the wave function – it may require multiple integrations which are very hard to perform even on a computer. Our team found a way to express a complete set of physical quantities in the form of a single determinant. This is a form far simpler than one would generally expect and which is easily tractable in practice.
Bootstrability
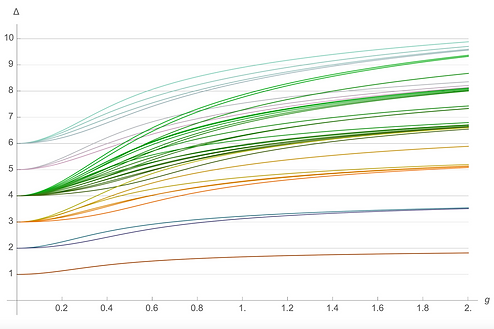
Approaching from the QFT side: Our team is also developing a new computational method which combines the information about the spectrum of the QFT, obtained from integrability, with the constraints of the conformal symmetry which the class of our QFT enjoys. Surprisingly we managed to successfully join these two approaches to obtain the most precise data to date for highly non-trivial important physical quantities. These results go well beyond the state of the art – no other existing method could obtain such accurate data in the fully-interacting regime of a field theory in four space-time dimensions. This result was reported on the most prestigious Strings conference this year.
Further Applications
The backbone of our advances is the QSC. Thus, understanding its hidden origins and broadening its applications would reinforce other directions of the project and strengthen the main results. Over the last year my team in collaboration with our colleagues from City, University of London and Surrey University discovered a new type of Quantum Spectral Curve with a more general mathematical structure. Based on this new advancement we conjectured a new QSC which describes an important set of 2D CFTs, which were at the forefront of theoretical physics for the last decade, but remained unsolved, nevertheless.
The project has already yielded several results which go beyond the state of the art:
- We discovered a new numerical method to calculate the physical quantities beyond the spectrum in a fully interacting 4D theory, which gives incredibly precise results.
- We developed a novel formal mathematical approach to study quantum spin chains, which revealed surprising simplicity, not expected previously.
- Finally, our team managed to apply our QSC method to a new class of holographic models, resolving the long-standing problem of exact integrability for strings moving in three dimensional anti-de-Sitter space.
There is still a rich area to be mined with the new methods we have developed: sharpening the numerical precision for a wider class of physical quantities in a 4D CFT; resolving the final obstacles to apply our analytic integrability based methods to 4D CFTs; and finding a plethora of new theories where our novel methodology can be effectively used. We also expect other groups of researchers to be driven in new directions by our successes and to join forces with us to uncover new discoveries. Ultimately, the project stimulates the shift in paradigm in QFTs, where strong interactions are no longer a problem in extracting predictions from an expanding class of quantum many-body systems.